What is Simulation model? Explain different types of simulation models?

Table of Contents

Model Classifications

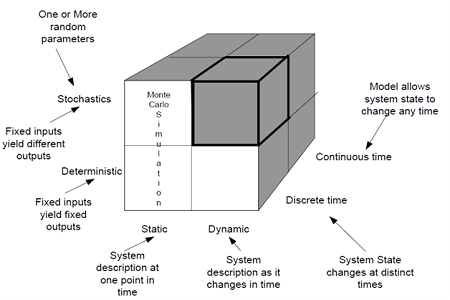
A few grouping classifications for models exist. A framework we are demonstrating shows probabilistic or stochastic system if a component of chance exists. For instance, the way of a tropical storm is probabilistic. Interestingly, a system can be deterministic, for example, the position of a falling item in a vacuum. Additionally, models can be deterministic or probabilistic.

A probabilistic or stochastic model displays arbitrary impacts, while a deterministic model does not. The consequences of a deterministic model rely upon the underlying conditions; and on account of PC usage with specific information, the yield is the same for each program execution. As we considered this and different modules, we can have a probabilistic model for a deterministic circumstance, for example, a model that utilizations irregular numbers to evaluate the region under a bend.

Discrete-Event Simulation Model

Adequate displaying ideas have been characterized with the goal that a discrete event simulation model can be characterized as one in which the state factors change just at those discrete focuses in time at which occasions happen. Occasions happen as a result of movement times and postponements.

Substances may go after framework assets, potentially joining lines while sitting tight on an accessible asset. Action and defer times may “hold” elements for terms of time. A discrete event simulation model is led after some time (“run”) by a component that propels mimicked time. The framework state is refreshed at every occasion alongside catching and liberating of assets that may happen around them.

Stochastic and Deterministic Systems

A framework shows probabilistic or stochastic system if a component of chance exists. Else, it displays deterministic system. A probabilistic or stochastic model shows irregular impacts, while a deterministic model does not.

Deterministic: Randomness does not influence the system of the framework. The yield of the framework isn’t an arbitrary variable.

Stochastic: Randomness influences the system of the framework. The yield of the framework is an irregular variable.

Static and Dynamic Simulations

We can likewise arrange models as static or dynamic. In a static model, we don’t consider time, with the goal that the model is practically identical to a depiction or a guide. For instance, a model of the heaviness of a lizard as being relative to the block of its length has factors for weight and length, however not for time.

By differentiating, in a dynamic model, time changes, so such a model is tantamount to an energized toon or a film. For instance, the quantity of lizards in a region experiencing improvement changes with time; and, subsequently, a model of such a populace is dynamic. A significant number of the models we consider in this content are dynamic and utilize a static segment as a component of the dynamic model.

A static model does not consider time, while a dynamic model changes with time.

Static: A reproduction of a framework at one particular time, or a simulation in which time isn’t a pertinent parameter, or instance, Monte Carlo and unfaltering state reenactments.

Dynamic: A reproduction speaking to a framework advancing after some time for cases, the dominant part of simulation issues.

Discrete vs. Continuous Systems

At the point when time changes constantly and easily, the model is persistent. On the off chance that time changes in incremental advances, the model is discrete. A discrete model is practically equivalent to a motion picture. A succession of edges moves so rapidly that the watcher sees movement. Nonetheless, in a live play, the activity is nonstop. Similarly as a discrete arrangement of motion picture outlines speaks to the consistent movement of on-screen characters, we frequently create discrete PC models of persistent circumstances .

In a Continuous model, time changes ceaselessly, while in a discrete model time changes in incremental advances.

Continuous: State factors change consistently as a component of time and for the most part diagnostic technique like deductive scientific thinking is utilized to characterize and understand the framework.